Физический размер матрицы фотоаппарата: На что влияет размер матрицы

На что влияет размер матрицы

На что влияет размер матрицы? Его обозначение в дюймах

Матрица или светочувствительная матрица — специализированная аналоговая или цифро-аналоговая интегральная микросхема, состоящая из светочувствительных элементов — фотодиодов.

• Предназначена для преобразования спроецированного на неё оптического изображения в аналоговый электрический сигнал или в поток цифровых данных (при наличии АЦП непосредственно в составе матрицы).
• Является основным элементом цифровых фотоаппаратов, современных видео- и телевизионных камер, фотокамер, встроенных в мобильный телефон, камер систем видеонаблюдения и многих других устройств.
• Применяется в оптических детекторах перемещения компьютерных мышей, сканерах штрих-кодов, планшетных и проекционных сканерах, системах астро- и солнечной навигации.

Обозначение матрицы характеризует геометрический размер чипа. Исторически сложилось, что маркировка матриц соответствует маркировке видиконов по внешнему диаметру с равным матрице размером чувствительной к свету области.

Обозначение не позволяет точно вычислять реальный размер матрицы (зато оно дает возможность сравнивать между собой матрицы различных типоразмеров). Понятно, что большая матрица имеет более крупные пиксели, чем маленькая, если количестве пикселей осталось прежнее.

Рассмотрим два примера.

Первый — это матрица компактного цифрового фотоаппарата с не самой маленькой матрицей 7.2 x 5.3 mm (обозначение 1/1.8″).

Второй — матрица зеркальной камеры 23.7 x 15.6 mm (обозначение «APS-C»).

При одинаковой пиксельности (в примере, у обоих матриц 48 квадратиков-пикселей), площадь каждого пикселя у крупной матрицы больше, и соответственно, светочувствительность и цветопередача у зеркалки куда лучше. На самом деле количество квадратиков-пикселей в реальных камерах гораздо больше, (например, 6 миллионов, а не 48 как здесь).

Для обозначения крупных (больше, чем 4/3″) матриц обычно используется так называемый кроп-фактор (Kf). Это отношение диагонали пленочного кадра 24х36 мм к диагонали данной матрицы. Матрицы, у которых Kf>1 часто называются «кропнутыми» (в отличие от «полнокадровых» матриц с Kf=1). Кстати, ЭФР = Kf * ФР.

Одна из важнейших характеристик, зависящих от размера матрицы — ее шумность. Так, ЦФК с матрицей APS-C (22×15 мм, Kf=1,6) позволяет устанавливать ISO в восемь раз больше, чем аппарат с матрицей 1/2.7″ (5,4х4,0 мм, Kf=6,4) при сохранении примерно одинакового уровня шумов. Отметим, что шум на изображениях также зависит от настроек повышения резкости (внутрикамерного шарпенинга) и шумоподава, поэтому матрицы одного типоразмера на разных камерах зачастую шумят по-разному.

Размер матрицы влияет и на ГРИП — чем больше матрица, тем меньше глубина резкости при равном угле зрения и одинаковом количестве пикселей. Кроме того, у больших матриц шире динамический диапазон, естественнее и натуральнее цвета.

К минусам крупной матрицы можно отнести, увеличенные размеры оптики, и рост цен. Поэтому чем более компактен аппарат и чем он дешевле, тем меньшего размера в нем установлена матрица.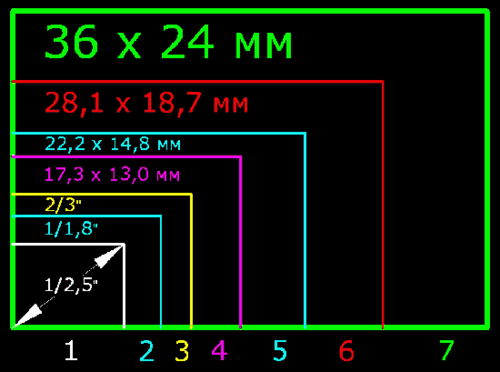

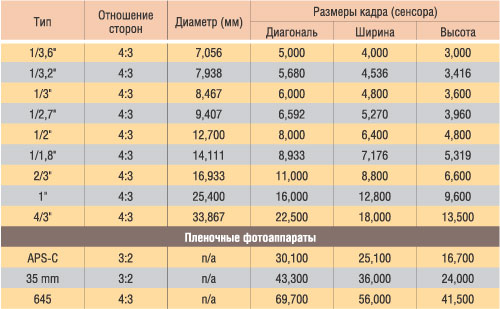
Ниже приведены наиболее распространенные типоразмеры матриц в сравнении с кадром 35 мм пленки:

Физический размер матрицы фотокамеры

В этой статье мы решили упорядочить и свести в таблицу размеры матрицы фотоаппарат для более лучшего понимания и определения матрицы фотоаппарата. Напомним, что матрица фотокамеры — это микросхема, состоящая из светочувствительных элементов — фотодиодов (пикселей). Она предназначена для преобразования спроецированного на неё оптического изображения в аналоговый электрический сигнал или в поток цифровых данных, который в последствии обрабатывается процессором фотокамеры и сохраняется в виде фотографии на карте памяти фотоаппарата. То есть матрица — это устройство фотокамеры, где получается изображение.

Физический размер матрицы фотокамеры — это ее геометрический размер — длина и ширина в миллиметрах. Однако, стоит отметить, что этот размер указывается ни в миллиметрах, а в обратном количестве дюймов.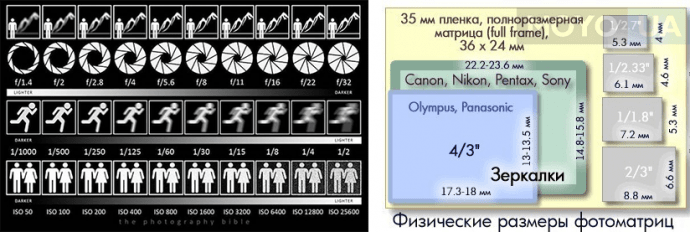 Например, 1/3.2, что соответствует

3.4*4.5 мм. Для выяснения физического размера матрицы стоит обратить внимание на следующую таблицу.

Пояснения к таблице: В первой колонке таблицы находится физический размер матрицы фотокамеры. Во второй, размер в её дюймах, принятый в спецификации. В третьей коэффициент, показывающий во сколько раз диагональ матрицы меньше диагонали кадра 35мм пленки обычного фильма (KF = 1).

Далее рассмотрим перечень матриц по типоразмерам:

• Матрицы размера 1 / 3.2″ — это самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 * 4.5 мм, используются в недорогих и компактных фотоаппаратах.
• Матрицы размером 1 / 2.7″ — соотношение сторон 4:3, физический размер 4.0 * 5.4 мм, используются в недорогих и компактных фотоаппаратах.
• Матрицы размера 1 / 2,5″ — соотношение сторон 4:3, то есть 4,3 * 5,8мм используются в большинстве компактных камер с несменной оптикой.
• Матрицы размера 1 / 1,8″ — соотношение сторон 4:3, геометрический размер 5,3 * 7,2 мм, используются в компактных камерах с несменной оптикой, среднего и выше среднего ценового диапазона (обычно в фотоаппаратах с разрешением от 8 Мпикс и более, но не обязательно).
• Матрицы размера 2 / 3″ — соотношение сторон 4:3, физический размер 6,6 * 8,8 мм иногда используются в дорогих компактных камерах с несменной оптикой.
• Матрицы размера 4 / 3″ — физический размер 18 * 13,5 мм, соотношение сторон 4:3, используются в дорогих камерах.
• DX, APS-C формат — соотношение сторон 3:2, размер около 24 * 18 мм. Матрицы таких размеров наиболее часто встречаются в цифровых зеркальных фотоаппаратах. Они соответствуют «полукадру» 35 мм кадра. Подавляющее большинство любительских, полупрофессиональных и даже профессиональных камер используют матрицы такого размера в силу того, что они относительно дёшевы в производстве и при этом размер пикселя остаётся довольно большим даже при 10 Мп разрешении.
• Полнокадровая матрица размера 36 * 24 мм — соотношение сторон 3:2, по размерам соответствующая классическому 35 мм кадру (3:2). На рынке представлено всего несколько моделей фотоаппаратов с матрицей такого размера. Такие матрицы дороги и сложны в производстве.
• Среднеформатная матрица формата 60 * 45 мм — соотношение сторон 3:2. Матрицы таких размеров «сшиваются» из матриц меньшего размера, что сказывается на их стоимости. Применяются в дорогих камерах.

Ознакомьтесь с обзором матриц, формирующих фотоизображение. Часть 1

Владимир Нескоромный

Главный редактор сайта alphapro.sony.ru

В потребительской технике всегда торжествует компромисс, о котором мы совершенно не задумываемся. Например, наше представление о передаче трехмерного пространства на плоской, двумерной фотографии, как правило, сводится к фокусному расстоянию объектива. Широкоугольник охватывает много объектов, телеобъектив — мало, кроме того, он уменьшает эффект пространственной перспективы. Но как, к примеру? 16-мм объектив, являясь широкоугольным для полнокадровой зеркалки, превращается в телевик для компактной камеры?

 

В поисках нормального объектива

Следует понимать, что характеристики объектива определяются не только (и не столько) его фокусным расстоянием, сколько размером светочувствительного элемента. В зависимости от эпохи, аналоговой или цифровой, это — кадр пленки или матрицы. Именно отношение фокусного расстояния объектива к диагонали кадрового окна и служит мерой нормальности объектива для фотоаппарата, с которым он используется. Если этот показатель значительно меньше единицы, объектив является широкоугольным, если больше — длиннофокусным, близок к единице — нормальный. Напомним, что для кадра 24х36 мм с диагональю 43,3 мм нормальными являются объективы с фокусным расстоянием f=40-60 мм; для среднего формата 6-см пленки граница нормальности f=70 мм; для полукадра 18х24 мм — f=30 мм.

 

Как формат определяет конечное качество изображения

Размер кадра пленки или матрицы определяет не только «перспективные» особенности получаемого изображения. В фотоиндустрии именно размер кадра, или формат, является компромиссным выбором, который необходим для выполнения различных требований. 

Во-первых, размер кадра определяет габариты самой камеры — большая или компактная. Во-вторых, размер кадра важен для достижения необходимой светочувствительности и детализации изображения. В-третьих, он косвенно определяет возможность и степень управления глубиной резкости. Например, в художественной портретной фотографии мы обычно стремимся к уменьшению глубины резкости. В пейзажной и технической, наоборот, к ее увеличению. В зависимости от того, какому требованию разработчики отдают предпочтение, реализуется то или иное решение.

Фотограф может снимать на форматные пленки и сканирующие задники с размерами в десятки сантиметров, когда камера достигает метровых габаритов. А сотрудник спецслужбы — использовать для выполнения задания миниатюрную камеру-пуговицу в запонке. Но каждый их них получает необходимый результат и совершенно не переживает из-за своих габаритов фототехники.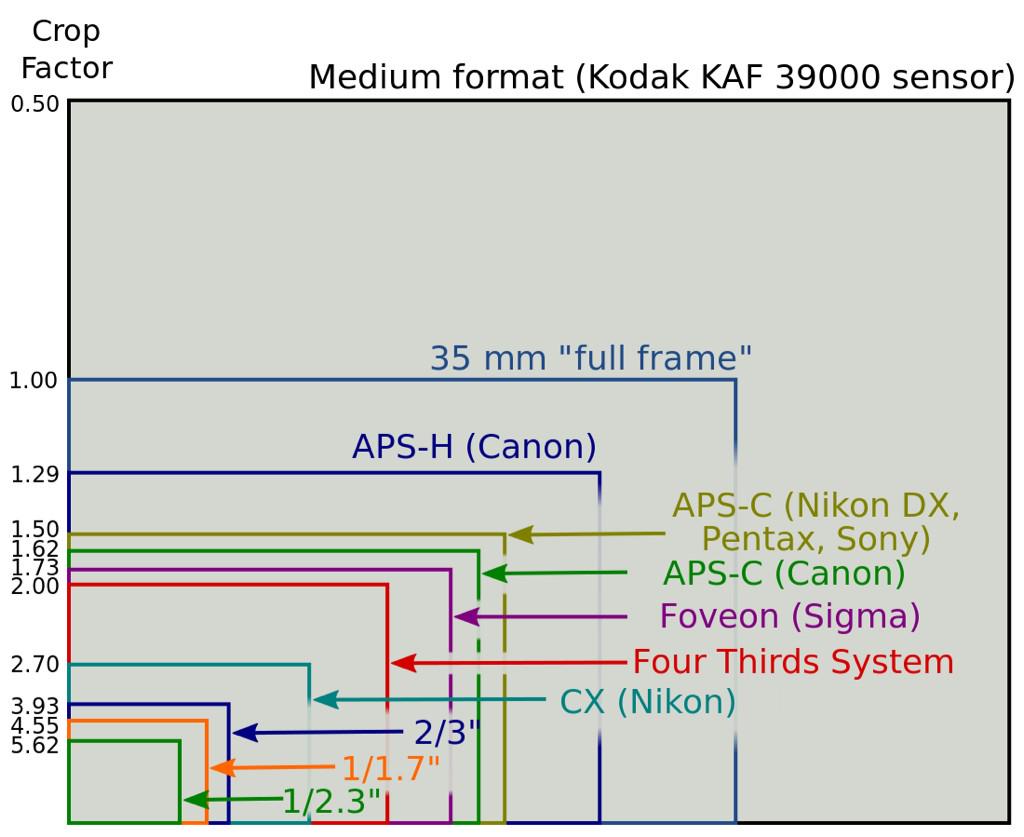

Характеристики объектива определяются не только его фокусным расстоянием, сколько размером светочувствительного элемента. Именно отношение фокусного расстояния объектива к диагонали кадрового окна и служит мерой нормальности объектива для фотоаппарата, с которым он используется. Если этот показатель значительно меньше единицы, объектив является широкоугольным, если больше — длиннофокусным, близок к единице — нормальный.

О минусах миниатюризации

Удобство использования камеры определяется возможностью ее транспортирования и выполнения съемочных настроек с помощью кнопок, дисков, тачпэдов и сенсорного экрана. Аппарат с 10-сантиметровыми габаритами кажется наиболее эргономичным, и кадр форматом в несколько сантиметров как раз ему подходит. Но если понадобится сделать компактный телезум-объектив, чтобы носить камеру в кармане, то кадр придется уменьшить. Однако тут же возникает масса проблем. При значительном уменьшении размера кадра станет весьма затруднительно реализовать сложную механику управления, юстировку оптики, сохранить достаточную светочувствительность и разрешение. На практике с этим сталкиваются обладатели недорогих смартфонов. Стремление к миниатюризации приводит к повышенным шумам, завалам резкости и контраста по полю кадра из-за неточной юстировки оптики.

 

Эпоха полного кадра

Следующее требование — обеспечение требуемого разрешения и светочувствительности. Изображение элемента снимаемого объекта регистрируется ячейкой сенсора или светочувствительным кристаллом пленки. Чем они (ячейка и кристалл) больше, тем больше светового потока смогут захватить. Соответственно, вполне закономерное желание — использовать светочувствительные элементы покрупнее. Однако возникает другая задача — разрешение, количество пикселей или кристаллов.

Чтобы увеличить разрешение, нужно увеличить размеры матрицы или кадра пленки. С пленкой проще — просто перейти на больший формат, например, 6х9 см или 4х5 дюймов.

А вот увеличивать размеры матрицы слишком дорого. Только к настоящему времени доступная цельная матрица доросла до полного кадра 24х36 мм.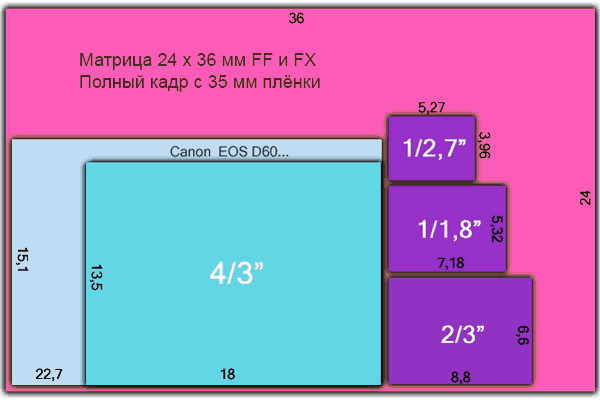 А ведь в свое время компании-производители даже сращивали две недорогие маленькие матрицы в одну большую. Например, такое решение было реализовано в камере Minolta RD-3000, выпущенной в 1999 году. В ней две матрицы по 1,5 Мпикс. с помощью призмы формировали изображение с финальным разрешением 2,7 Мпикс.

 

Ограничения в гонке мегапикселей

Чтобы повысить разрешение, приходится уменьшать размер регистрирующего элемента сенсора при сохранении формата матрицы. К сожалению, и для пленки, и для матрицы существует физический предел уменьшения размера отдельного элемента. А значит, что и у разрешения тоже есть свой предел. Речь идет о дифракционном рассеянии света, обусловленное ограниченностью размера объектива. Оно накладывает ограничение на минимальный шаг между светочувствительными элементами матрицы.

Например, чтобы раскрыть потенциал по разрешению объектива с диафрагмой f/2, достаточно использовать матрицу с минимальной дистанцией между светочувствительными элементами около одного микрона.

Использовать матрицу с шагом меньше 3 микрон с оптикой со светосилой f/5.6 не имеет смысла, поскольку пятно дифракционного рассеяния растет пропорционально диафрагменному числу.

В случае с пленочной фотографией ограничением на разрешение является структура фотоэмульсии. Хотя размер светочувствительного кристалла современных пленок и близок к одному микрону, но их распределение в слое эмульсии толщиной в несколько микрометров ограничивает разрешающую способность обычной фотопленки примерно 10 микронами (100 линий/мм).

 

Маленькие шаги на пути к гигантскому разрешению

А что происходит в цифровой фотографии, где матрица с шагом в один микрон уже стала реальностью? Попробуем оценить желаемую мегапиксельность полнокадровой матрицы 24х36 мм с шагом ячеек в один микрон применительно к объективу со светосилой f/2.

Тысяча элементов на миллиметр в пересчете на общее разрешение матрицы составят 24000х36000 или почти 900 Мпикс.! К сожалению, современная электроника не способна поддерживать такую матрицу, а именно, эффективно считывать и сохранять получаемый гигантский объем информации. Про массовый выпуск таких матриц мы даже не говорим.

В настоящее время в системных камерах Sony устанавливают полнокадровые матрицы с разрешением 42,4 Мпикс. и шагом 4,5 микрона (ILCE-7RM2). Имеет ли смысл дальнейшее повышение разрешения? С точки зрения потребителя, несомненно. Однако с инженерных позиций, при современном уровне развития технологий вряд ли будет оправданным стремление к повышению разрешения до дифракционного предела. Неидеальность оптики (аберрации и ошибки юстировки, фокусировки) устанавливает свои, более грубые, чем дифракционный предел, ограничения на увеличение разрешения.

В тоже время компания Sony наращивает линейку объективов серии G Master, которые способны поддерживать матрицы с разрешением в 100 Мпикс. Неужели нас ждет очередная сенсация?

Ну, а маленькие матрицы с шагом, близким к одному микрону, успешно используются в цифровых компактах и смартфонах.

Полнокадровая матрица в камере Sony A7R II. Разрешение 42,4 Мпикс.

О плюсах и минусах глубины резкости

Наконец, третья характеристика фотоизображения — глубина резкости. Для начала вспомним, что такое гиперфокальное расстояние. Мы видим резкими объекты не точно на дистанции наводки на резкость, а в некотором диапазоне около нее. И можно выбрать дистанцию наводки объектива так, что при установленной диафрагме все объекты от точки наводки на резкость и до бесконечности будут казаться резкими. Эта дистанция и есть гиперфокальное расстояние. Как правило, оно пропорционально квадрату фокусного расстояния и обратно пропорционально диафрагменному числу.

Если сравнивать результат, получаемый двумя камерами — с маленькой и большой матрицей, то окажется, что при равных условиях (угол охвата пространства и размер конечной картинки) гиперфокальное расстояние для камеры с меньшим фокусным расстоянием и небольшой матрицей будет меньше. Иными словами, при той же диафрагме на снимке компактной камеры зона резкости будет находиться ближе и будет шире, чем у камеры с большой матрицей. Это означает, что диафрагма f/2 компакта, на самом деле, вовсе не дает портретного эффекта с малой глубиной резкости, а работает как f/8-11 зеркалки или беззеркалки.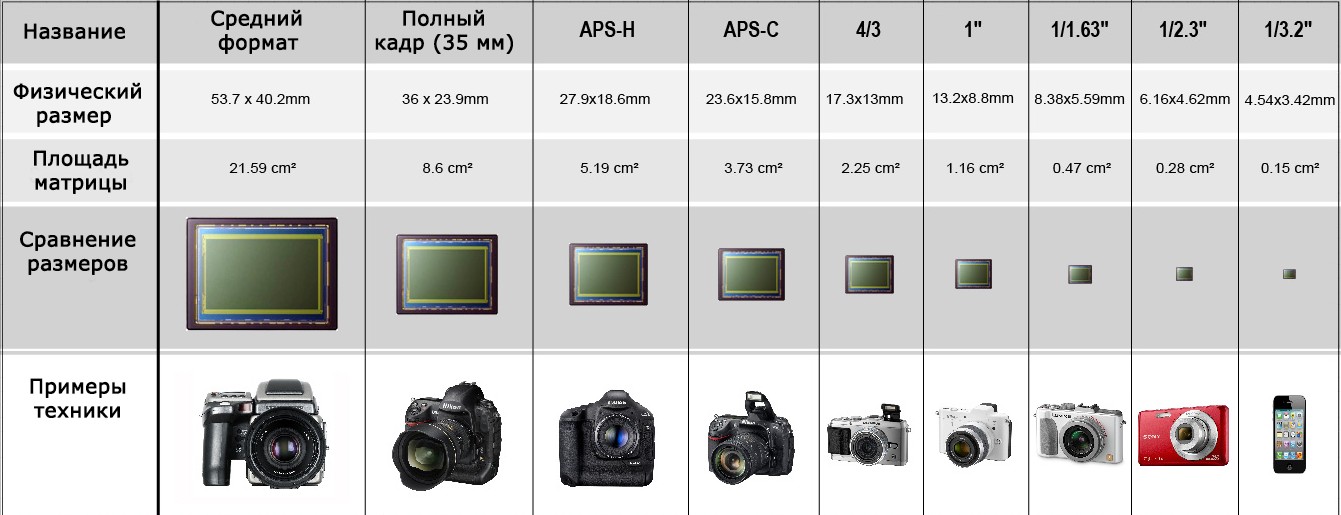

Для портретов это, может быть, и не очень здорово, а для предметной и макросъемки, наоборот, просто замечательно. Ведь за увеличение глубины резкости не нужно платить диафрагмированием объектива, длинной выдержкой, повышением светочувствительности и, в конце концов, чистотой картинки (шумами) и резкостью.

 

Заключение

На фоторынке сейчас можно встретить самые различные предложения. Однако чтобы хорошо ориентироваться в них, следует знать основные параметры фототехники и понимать важность каждого их низ применительно к своим задачам. Собственно, мы их изучили. Теперь можно переходить к выбору конкретной камеры, и этой теме посвящен следующий материал.

 

Продолжение материала (часть 2) читать здесь.

Как узнать размер пикселя матрицы?

© 2016 Vasili-photo.com

Для чего фотографу может потребоваться размер пикселя? Таких ситуаций хватает. Знание размера пикселя бывает полезно для определения безопасной выдержки при съёмке с рук, ведь чем мельче пиксель, тем заметнее на снимках проявляется дрожание камеры, и тем более короткая выдержка может потребоваться для устранения шевелёнки.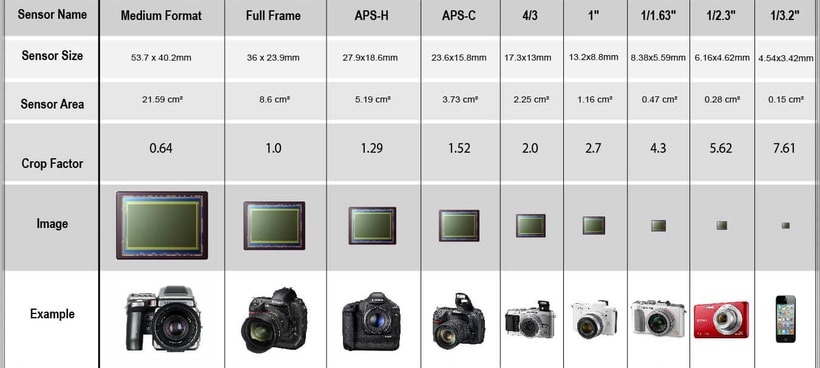 Не имея представления о размере пикселя матрицы вашего фотоаппарата, нельзя всерьёз рассуждать о глубине резкости, поскольку именно от размера пикселя напрямую зависит допустимый диаметр кружка рассеяния. Значение дифракционно-ограниченной диафрагмы для конкретной фотокамеры также зависит от размера пикселя. Наконец, не исключено, что при сравнении нескольких камер вы захотите узнать, какая из них обладает большей плотностью пикселей, а, значит, обеспечивает лучшую детализацию и больше подходит для съёмки удалённых объектов.

В инструкциях к цифровым фотоаппаратам очень редко указывается размер пикселя матрицы, но, к счастью, этот параметр довольно легко рассчитать самостоятельно.

В большинстве инструкций можно найти сведения о физическом размере фотоматрицы, а также о её линейном разрешении, т.е. о количестве пикселей, умещающихся на матрице в одном ряду по горизонтали или по вертикали. Например, матрица цифрового фотоаппарата Canon EOS 70D имеет размеры 22,5 × 15 мм или 5472 × 3648 пикселей. Чтобы найти размер одного пикселя, достаточно взять цифры для любой из сторон, разделить миллиметры на пиксели и умножить полученное частное на 1000, чтобы перевести результат в микрометры (микроны). Получаем формулу:

, где

n – размер пикселя в микрометрах;

x – линейный размер матрицы в миллиметрах по одной из сторон;

a – количество пикселей по соответствующей стороне.

Для упомянутого выше 70D расчёт будет следующим:

22,5 ÷ 5472 · 1000 ≈ 4,1 мкм

Результат округлён до 0,1 мкм. Этого более чем достаточно для любых практических целей. Я использовал длинную сторону матрицы, но вы можете взять короткую и убедиться в том, что результат будет идентичным. У всех массовых современных фотоаппаратов пиксели условно квадратные, и потому расчёты можно проводить по любой из сторон матрицы. Впрочем, при использовании длинной стороны погрешность вычисления оказывается несколько меньше.

Возможно, вам не хочется лезть в инструкцию? Что ж, размер пикселя можно вычислить и не зная точных размеров матрицы.

Вам достаточно вспомнить разрешение вашей камеры в мегапикселях и её кроп-фактор. Уж эти-то параметры своего аппарата знает любой фотолюбитель. Формула будет выглядеть следующим образом:

, где

n – всё тот же размер пикселя в микрометрах;

K_f– кроп-фактор;

N – разрешение в мегапикселях.

Таким образом, для Canon EOS 70D, обладающего кроп-фактором 1,6 и разрешением 20 Мп получаем:

29,4 ÷ (1,6 · √20) ≈ 4,1 мкм

Как видим, обе формулы дают абсолютно единодушный ответ. Вы вправе использовать ту, которая вам больше нравится.

На случай, если кто-то из моих читателей не в ладах с квадратными корнями, я счёл своим долгом самостоятельно рассчитать размеры пикселей для некоторых наиболее употребимых цифровых форматов и свести эти данные в единую таблицу. Пользуйтесь на здоровье.

Размер пикселя в зависимости от разрешения камеры и её кроп-фактора, мкм.

Разрешение, Мп	Кроп-фактор
	1*	1,5	1,6	2	2,7
10		6,2	5,8		3,4
12	8,5	5,7	5,3	4,2
14		5,2			2,9
16	7,3	4,9		3,7
18	6,9		4,3		2,6
20	6,6		4,1		2,4
21	6,6	4,2
22	6,4
24	6	4	3,8
28		3,7
30	5,4
36	4,9
42	4,5
45	4,4
50	4,1

* Кроп-фактор, равный единице, соответствует
полному кадру (36 × 24 мм).

Очевидно, что чем меньше матрица цифрового фотоаппарата и чем выше его разрешение, тем меньшим размером обладает единичный пиксель матрицы. Хорошо это или плохо?

Главным, да, пожалуй, и единственным положительным следствием уменьшения размеров отдельного пикселя является возрастание общей плотности пикселей. Матрица с большей плотностью пикселей при прочих равных условиях способна обеспечить лучшую детализацию снимка. Однако это преимущество, хоть и довольно весомое, тянет за собой целый ворох негативных последствий. Камеры с высоким разрешением очень требовательны к качеству объективов и техническому мастерству фотографа. Они не прощают небрежности в работе и с циничным удовольствием запечатлят на снимке не только полезные детали, но и всевозможные дефекты оптики, шевелёнку и промахи фокусировки. Чем мельче пиксель, тем раньше становится заметным негативное влияние дифракции на резкость при диафрагмировании объектива. Вместе с тем, мелкий пиксель диктует пропорционально малые размеры допустимого кружка рассеяния, уменьшая тем самым глубину резко изображаемого пространства.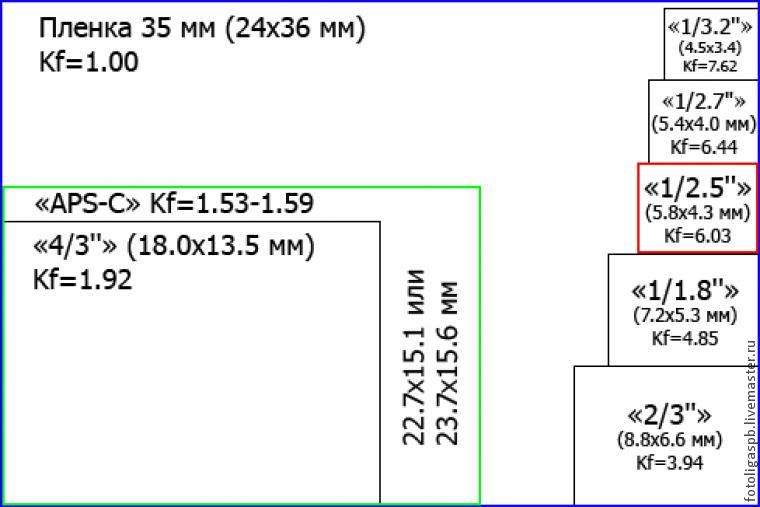

Следует помнить, что при двукратном уменьшении линейных размеров пикселя его площадь уменьшается вчетверо, а, значит, вчетверо же уменьшается и количество фотонов, которые способен уловить фотодиод в единицу времени. На практике это означает падение ёмкости фотодиода, и пропорциональное снижение динамического диапазона матрицы. Можно даже сказать, что повышение количества пикселей почти всегда осуществляется ценой снижения их качества.

***

Не исключено, что у некоторых читателей возникнет вопрос: а действительно ли автор уверен в том, что размер пикселя может быть рассчитан с помощью приведённых им формул? Нет, автор в этом не уверен. Собственно фотодиоды матрицы занимают далеко не всю её площадь, и их фактический размер всегда меньше расчётного (см. «Как работает цифровой фотоаппарат»). Если быть точным, то формулы наши позволяют вычислить расстояние между геометрическими центрами двух соседних фотодиодов. Это расстояние смело может быть принято за теоретический размер пикселя и использовано для любых необходимых фотографу вычислений.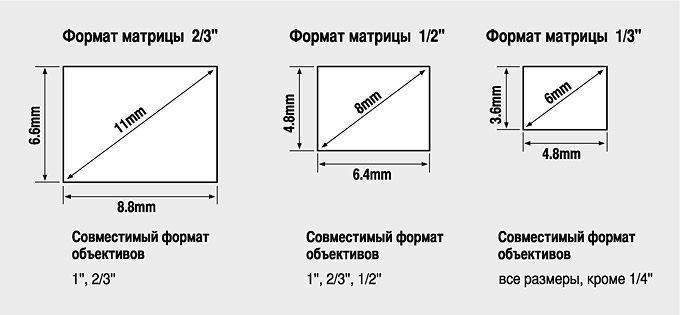

Спасибо за внимание!

Василий А.

Post scriptum

Если статья оказалась для вас полезной и познавательной, вы можете любезно поддержать проект, внеся вклад в его развитие. Если же статья вам не понравилась, но у вас есть мысли о том, как сделать её лучше, ваша критика будет принята с не меньшей благодарностью.

Не забывайте о том, что данная статья является объектом авторского права. Перепечатка и цитирование допустимы при наличии действующей ссылки на первоисточник, причём используемый текст не должен ни коим образом искажаться или модифицироваться.

Желаю удачи!

Дата публикации: 07.01.2015   Последнее обновление: 11.11.2016

Вернуться к разделу «Матчасть»

Перейти к полному списку статей

Как выбрать цифровой фотоаппарат. Сколько должно быть мегапикселей

Матрица фотоаппарата

Матрица — один из самых значимых элементов фотоаппарата. В цифровых фотоаппаратах заменяет пленку и представляет из себя плоскую (пока) панельку, содержащую на своей поверхности ячейки — пиксели. Ячейки собирают фотоны света и преобразовывают их в электрические сигналы, которые считываются электроникой камеры и оцифровываются. Но таким образом определяется только количество света, а не его цвет. Чтобы получить цветной пиксель каждая ячейка матрицы прикрыта светофильтром и получает свет только одного из трех основных цветов.

Матричный цветофильтр.

Это общие принципы устройства сенсоров, но различаются они не только количеством пикселей, а еще и геометрическими размерами. И если профессиональная камера оборудуется полнокадровой матрицей, т. е. ее геометрические размеры эквивалентны размеру 35 мм пленки — 36 х 24 мм, то в вашем смартфоне она значительно меньше.

Физические размеры сенсоров

Понятно, что при одинаковом количестве ячеек, но значительно меньших геометрических размерах сенсора, каждая ячейка тоже становится значительно меньше.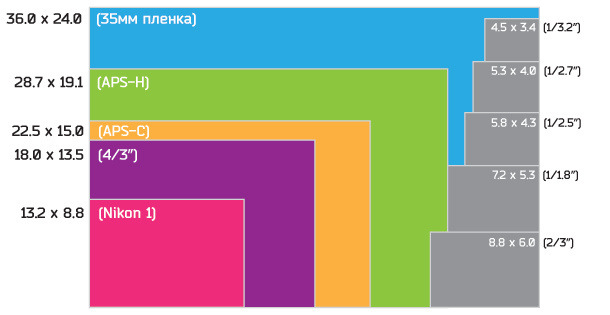 Вместе с тем падает ее способность улавливать фотоны света, т. е. она хуже «видит» — падает ее чувствительность. Низкая чувствительность сенсора означает потерю данных и увеличение цифрового шума при недостаточном освещении (шум это разноцветные точки в полученных снимках). Процессор фотоаппарата борется с шумами, но в результате работы «шумодава» снижается качество изображения, оно «замыливается».

С уменьшением площади отдельных ячеек сенсора, падает четкость изображения в мелких деталях. Связано это с тем, что при прохождении в отверстие диафрагмы объектива лучи света отклоняются, образуя на поверхности матрицы центрические круги, так называемый диск Эйри. Диаметр этого диска (кружка рассеивания) зависит только от диаметра отверстия диафрагмы, но если становится сравним с размером пикселя камеры (или предельно допустимого кружка нерезкости), он начинает оказывать визуальное влияние на изображение. Если два диска Эйри оказываются расположены ближе половины их размера, они сливаются в один.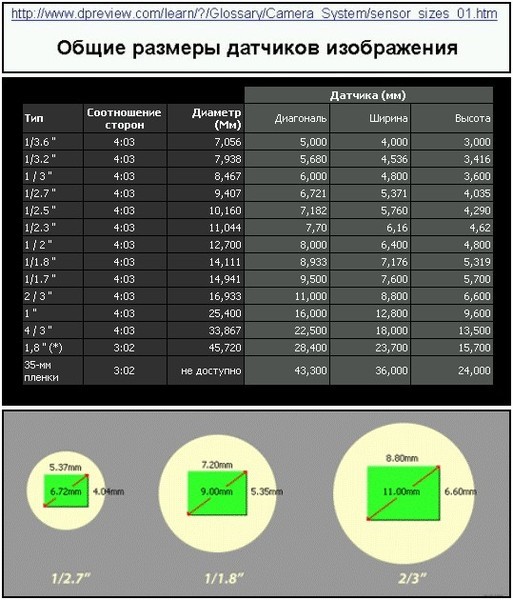

Кружок рассеивания на матрице с разными размерами пикселя

Уроки фотографии для начинающих. Выбор фотоаппарата

Выбор камеры — в большинстве случаев вопрос субъективный. Фотоаппарат — это не мобильный телефон и не карманный компьютер, от которого требуется, чтобы он «умел» то-то и то-то. Если вы собираетесь именно снимать, а не хвастать перед друзьями, какая у вас «крутая камера», то для вас будет куда важнее, как камера лежит в руке, насколько хорошо конечное качество картинки, как автоматика справляется со сложными условиями, чем то, сколько у нее мегапикселей, какова кратность зума и какого размера дисплей.

Технические характеристики важны — но нужно обращать внимание только на те из них, смысл которых вы точно понимаете и которые вам реально требуются. Если за одну и ту же цену предлагаются две камеры, одна с трехкратным оптическим зумом, двухдюймовым дисплеем и 6-мегапиксельной матрицей, а вторая — с двенадцатикратным оптическим зумом, трехдюймовым дисплеем и 12-мегапиксельной матрицей, то стоит серьезно задуматься. Бесплатным, как известно, бывает только сыр в мышеловке, а наиболее дешевый способ сделать камеру более привлекательной — это увеличить несколько цифр характеристик, не сильно заботясь о качестве в целом. Возможно, в первой модели и оптика будет получше, и конструкция понадежнее, и эргономика поприятнее. Просто повертите в руках обе модели (магазинов, где дают посмотреть портативную технику перед покупкой, сейчас достаточно), посмотрите тестовые снимки, поснимайте сами.

Чтобы сделать цифры еще более привлекательными, часто идут в ход округления и приписки. «Округляют» многие показатели, но чаще всего разрешение матрицы. Допустим, максимальное разрешение фотографии — 3600×2630. Реальное разрешение — 9,46 Мп. А в документации пишут: «Эффективное разрешение — 10,0 Мп». При этом не стесняются рядом указывать максимальное разрешение снимка, хотя термин «эффективное разрешение» как раз обозначает реальный размер получаемой картинки, а для указания общего числа мегапикселей существует параметр «полное разрешение». Оно и понятно: 10-мегапиксельную камеру купят скорее, чем 9,5-мегапиксельную, и на рекламном проспекте «круглые» цифры писать удобнее.

С зумом еще веселее. Здесь уже иногда встречаются не только округления, но и приписки. Известно что есть оптический и цифровой зум. Оптический зум осуществляется самой оптической системой, а цифровой — просто растягивает полученную картинку. Действие довольно бессмысленное, которое в любом редакторе можно сделать, причем куда более качественно и аккуратно. Поэтому почти всегда и пишут в спецификации: «3x оптический, 10х цифровой зум» — всем все понятно, никто не обижается. Однако бывают случаи, когда обе спецификации заменяют на единственную,типа Mega-Super-Intellectual 30x zoom. И только где-нибудь на англоязычном сайте, в разделе для разработчиков, на 254 странице руководства, внизу мелким шрифтом — указывается, что технология Mega-Super-Intellectual zoom подразумевает сочетание 3-кратного оптического зума с «умной» 10-кратной интерполяцией. Весело, правда? Интерполяция, какой бы «умной» она ни была, не в состоянии «нарисовать» детали там, где их нет, а если и пытается — то выглядеть это будет, в любом случае, довольно убого.

Менее запущенная стадия того же самого — иногда указывается «цифровой зум без потери качества». Справедливой эта фраза будет только в одном случае: если оптика фотоаппарата и без того достаточно «мыльная». В этом случае небольшая интерполяция действительно не сделает картинку хуже.

Кстати, встречается и опускание некоторых не особенно привлекательных цифр из характеристик. Так, если производитель «забывает» указать физический размер матрицы (параметр, кстати, не менее, а то и более важный, чем разрешение) — почти наверняка матрица будет не больше 1/2,5″. В принципе, в этом нет ничего страшного — чуть повыше уровень шумов, и все. Но если на этих 1/2,5″ ухитряются разместить 12 и более мегапикселей — уровень шумов уже будет не просто высоким, а очень высоким.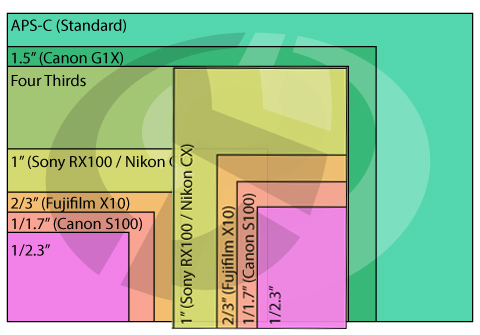 И «забыть» указать маленький физический размер матрицы, при этом крупно написав на корпусе камеры 12 MegaPixels — на наш взгляд, не совсем порядочно. Отговорки, что «большинству пользователей это неинтересно» при этом не работают: кому не интересно, для тех есть раздел «сокращенная спецификация», а кому интересно — в любом случае должны знать.



Уроки фотографии для начинающих. Главная.

Использование материалов разрешено только при условии размещения активной ссылки на сайт www.photo-lesson.ru

Про размеры матриц фотоаппаратов — Журнал Плотника — LiveJournal

Вот современные фотоаппараты. Ну, речь не о мыльницах, а о (полу)профессиональной технике — зеркалки, беззеркалки, дальномерки. Средний и большой цифровой формат рассматривать не будем по причине неметрической стоимости 🙂

У подавляющего большинства размер матрицы — 23.5mm на 15.6mm (с небольшими вариациями — у Кенона она чуть поменьше) или полноразмерные 36mm x 24mm.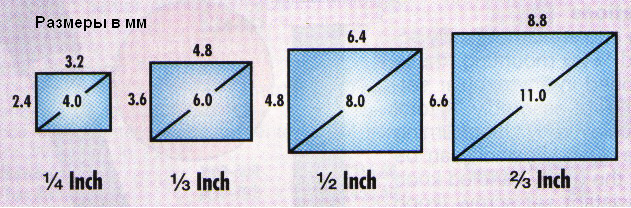

А ведь это совершенно дурацкий, если разобраться, размер. Это соотношение сторон 2:3. Он только у одного формата бумажной фотографии такой — у кретинского 4 x 6in (10 x 15cm в Европах). Это весьма распространённый размер, по причине того, что один из самых дешёвых, его в любом минилабе любая собака тебе напечатает. Но любой человек, который снимал фотографии хорошего качества, а потом их печатал, знает, что на отпечатке 10 х 15 не видно вообще нихрена. И что фотографу, как художнику, очень обидно — из прекрасного снимка получается мелкота, где теряются все детали. И что напечатанная даже 5 x 7in (13 x 18cm) — она часто уже смотрится лучше. А напечатанная 8in x 10in (20 x 25cm) — ещё лучше. А уж 11 x 14in (28 x 36cm) — вообще красота, всё рассмотреть можно.

Но последние два размера вообще чуть ли не квадратные. Соответственно, при печати фотографии 8in x 10in (20 x 25cm) со стандартной матрицы фотоаппарата мы теряем почти 20% полезной площади сенсора! И фотографию приходится художественно перекадрировать под необходимый размер каждый раз. Дурево? Дурево.

Причина — как обычно, технический консерватизм, ибо ноги у современных популярных камер растут из камер плёночных, где кадр 36mm x 24mm обуславливался самим фотографическим материалом. Хотя никто вообще не запрещает сделать матрицу абсолютно любого размера и формата — хоть шестиугольную. Была бы моя воля — я бы делал фотоаппараты с квадратной матрицей или матрицей 4:5.

Немного изменить существующую ситуацию попробовал Олимпус. Они создали свой формат 4/3, но сделали его через задницу — ибо диагональ стандартного сенсора формата 4/3 ещё меньше, чем у кропнутого сенсора (кроп-фактор 2 вместо 1.5-1.6). Объяснять, чем меньший физический размер матрицы хуже — надеюсь, не надо.

Нет в жизни щасья!!!

У профессиональных цифровых камер среднего формата — например, Мамия 645ДФ+ размер матрицы, кстати ПРАВИЛЬНЫЙ — 56×41.5mm, то-есть практически 4:5. Но стоит такая камера — неметрически, под пять тыщ монет.

Хотя никто в принципе, не запрещает воткнуть матрицу с соотношением сторон 4:5 в обычный фотоаппарат.

Размер пикселя и матрицы, его разрешение и апертура в камере смартфона

Популярность смартфонов стремительно растет уже более 10 лет. Конечно, компании адекватно реагируют на огромный спрос, постоянно совершенствуя свои модели. Традиционно конкурентоспособность любого устройства зависит от его цены, функциональности и характеристик. Цена и функциональность в этой статье не рассматриваются. Но в целом конкуренция вынуждает компании интенсивно расширять функциональность и проводить гибкую ценовую политику.В итоге современный бюджетный смартфон стоимостью несколько сотен долларов уже предоставляет возможности, которые кажутся безграничными по сравнению с моделями 5-летней давности.

Blackview MAX 1 Проектор Мобильный телефон с функцией проектора, режим рабочего стола в Android Q 10 и складные смартфоны прекрасно иллюстрируют эту тенденцию. Фактически, современный смартфон превратился в универсальный карманный компьютер с довольно качественными мультимедийными функциями, включая камеру, проектор и т.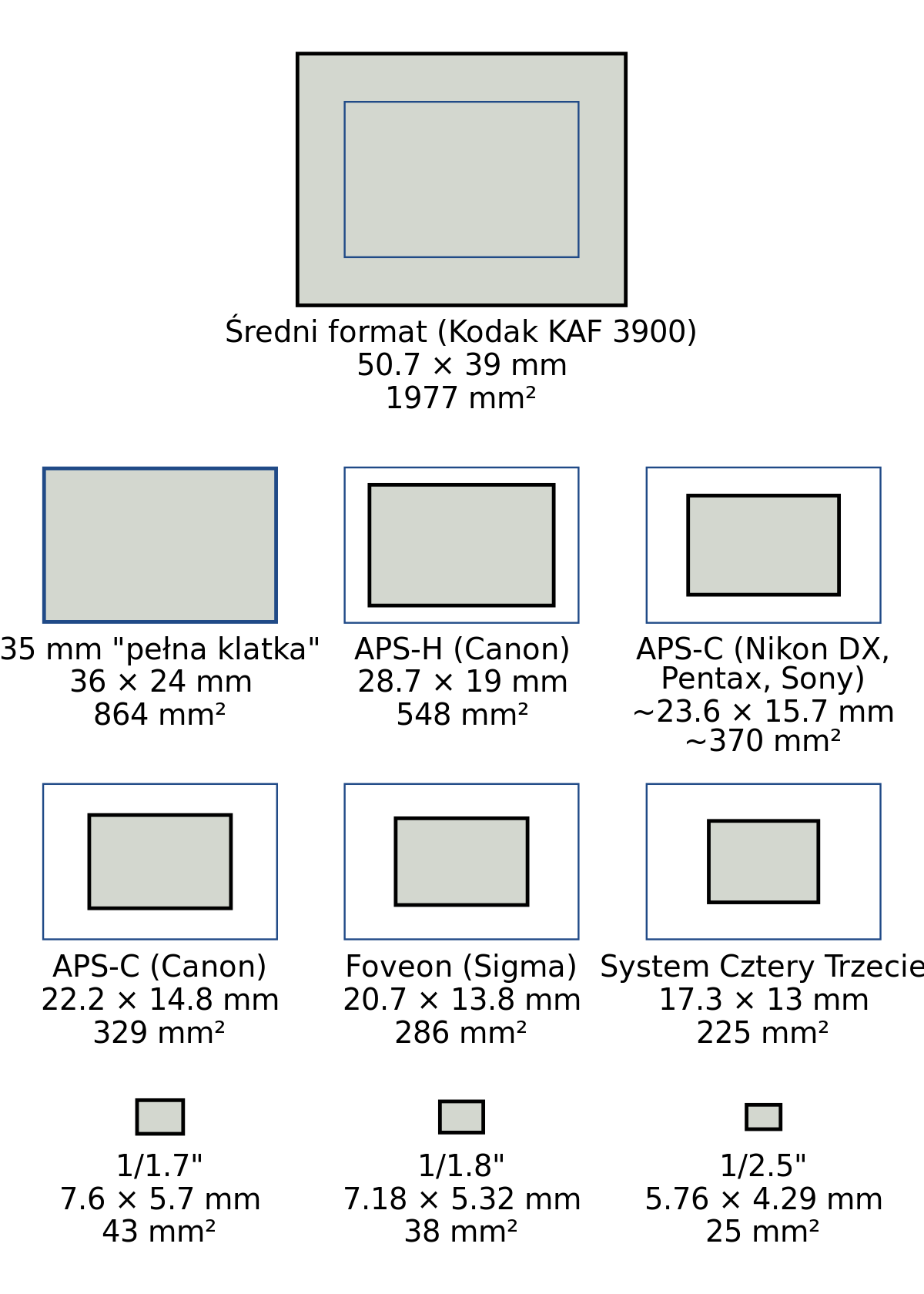 Д.

Конечно, конкурентоспособность требует постоянного улучшения всех компонентов, включая производительность смартфона, камеру, хранилище смартфона, ОС, экран и т. Д.В частности, усовершенствование фотоаппаратов развивается по двум направлениям.

Во-первых, компании увеличивают количество различных фотоаппаратов, расширяя возможности съемки. В результате современные многокамерные смартфоны обеспечивают высокое качество изображения при съемке практически в любых условиях. Список самых популярных дополнительных модулей включает камеры Ultra-Wide, Telefoto, Depth и ToF.

Сегодня даже в бюджетных моделях часто используются две камеры. Современные флагманы обычно имеют три и более модулей.Более того, Sony анонсировала смартфон с невиданными ранее 8 камерами.

Во-вторых, компании традиционно продолжают улучшать основные характеристики матриц и линз. В данной статье предлагается более подробный анализ этого аспекта.

Разрешение, размер пикселя и апертура

Как известно, матрица формирует изображение с помощью светочувствительных ячеек (фотодатчиков).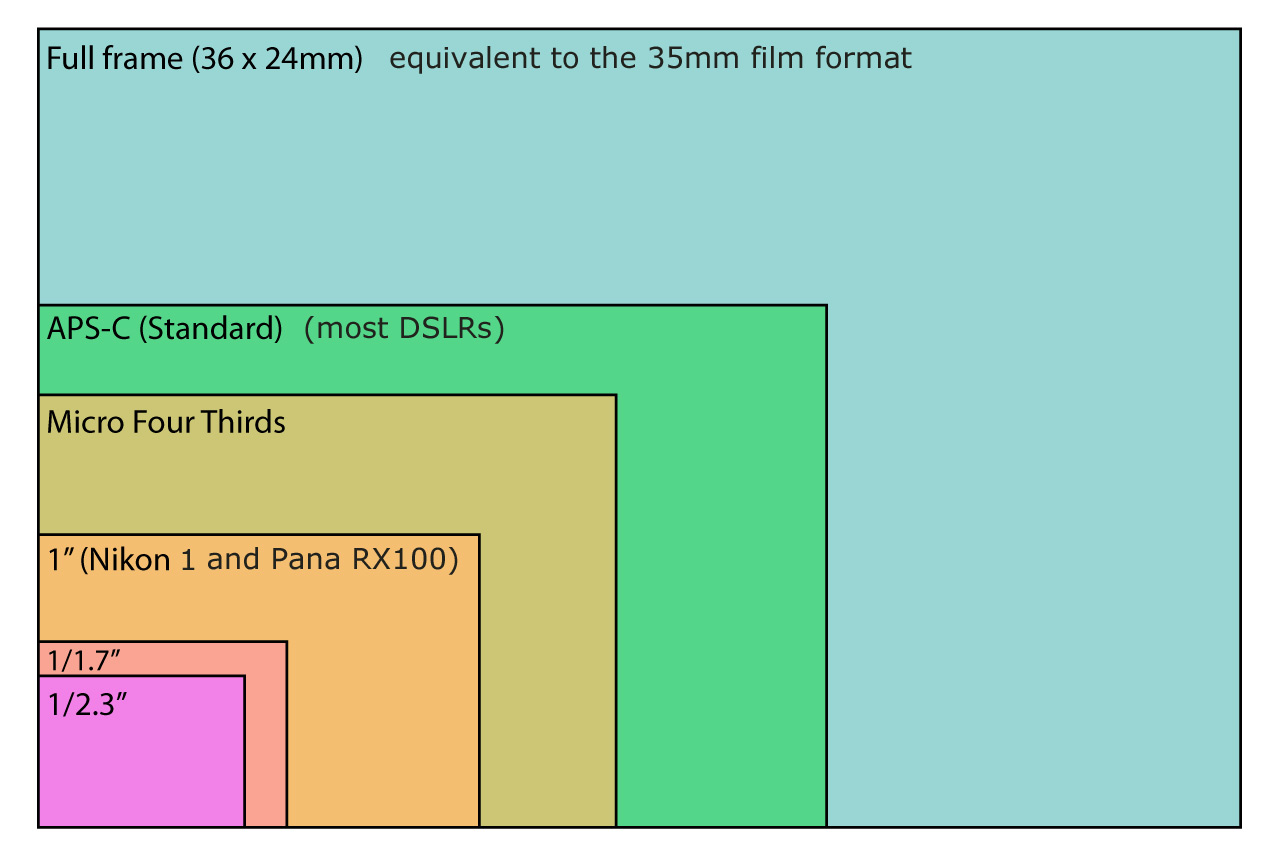 1 МП соответствует миллиону фотодатчиков на матрице. Они определяют разрешение матрицы и напрямую влияют на качество изображения.

Несколько лет назад в смартфонах в основном использовалась 0,5-, 1,3-мегапиксельная или 2-мегапиксельная матрица. Лишь у некоторых флагманов были камеры на 5 МП. Стремительное развитие технологии производства фотосенсоров в корне изменило ситуацию. В современных моделях уже используются матрицы с разрешением от 8 МП до 40 МП и даже больше.

Размер пикселя напрямую влияет на количество поглощенных фотонов во время экспонирования. Соответственно, эффективность захвата потока фотонов различна для матриц с разными размерами пикселей.Этот фактор напрямую влияет на качество изображения. Его градации:

— 1,55 мкм-1,40 мкм — высокое качество даже при слабом освещении;

— 1,40 мкм-1,22 мкм — высокое качество при нормальном освещении, шумы изображения при слабом освещении;

— 1,12 мкм или меньше — высокое качество только при ярком освещении.

Но увеличение размера пикселя при том же разрешении требует увеличения размера матрицы и оптики, что увеличивает толщину и ширину смартфона. Поэтому компании вынуждены постоянно искать компромиссные решения.

Яркие детализированные изображения требуют мощного светового потока, который зависит от диафрагмы (степени открытия объектива).

Соответственно, широкая апертура поглощает больше светового потока. Его размер обозначается буквой «f». Широкая диафрагма обеспечивает макросъемку, эффект боке и т. Д.

Влияние диафрагмы на качество:

— f / 2.6, f / 2.4 — низкое качество;

— f / 2.2, f / 2.0 — обычно используются в бюджетных моделях;

— f / 1.8, f / 1.7, f / 1.6 — оптимальная диафрагма.

Размер датчика изображения

Матрица представляет собой микросхему со светочувствительными фотодиодами. Как известно, фотодиод под действием света формирует электрический сигнал, который впоследствии преобразуется в цифровой сигнал. Фактически матрица выполняет функцию пленки в традиционных фотоаппаратах. В дальнейшем информация об изображении поступает в процессор, который преобразует его и отправляет в хранилище смартфона. В среднем этот процесс длится 0,2-0,3 секунды.

При этом качество картинки напрямую зависит от размера матрицы.

В современных моделях используются матрицы со следующей диагональю:

— 1/3 ″ — бюджетные смартфоны;

— 1 / 2,9 ″, 1 / 2,8 ″ — модели среднего уровня;

— 1 / 2,6 ″, 1 / 2,3 ″ — флагманские смартфоны.

Например, диагональ 12-мегапиксельной матрицы Sony IMX386 в Xiaomi Mi Mix 2 составляет 1 / 2,9 ″ (6,2 мм), а размер пикселя — 1,25 мкм.

Соотношение между размером матрицы и пикселем

Конечно, большое количество пикселей (разрешение) требует увеличения их плотности.

Но для постоянного размера матрицы это требует уменьшения размера пикселей с уменьшением поглощения света каждым из них. Таким образом, только выбор оптимального соотношения сторон может обеспечить максимальное качество изображения.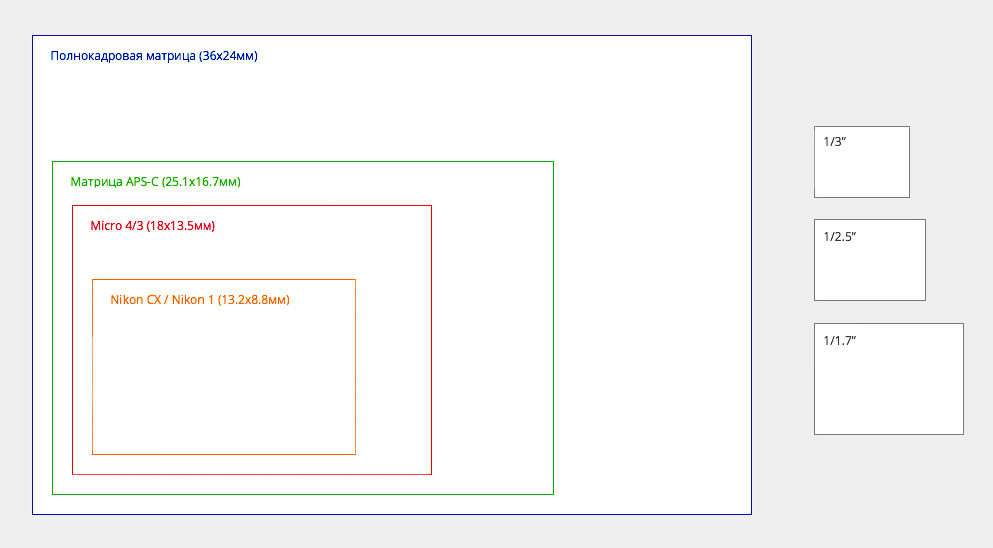

Из маркетинговых соображений большинство компаний часто не указывают размер пикселей, указывая только разрешение матрицы. Но разрешение не характеризует эффективность светопоглощения, а, как следствие, реальное качество снимков.

Сегодня компании экспериментируют с этим соотношением.Samsung Galaxy S6 отлично продемонстрировал очень удачное сочетание.

При тех же характеристиках он явно выигрывает по сравнению с iPhone 6.

Кроме того, Samsung Galaxy S7, S8, S9 с 12-мегапиксельной матрицей также демонстрируют отличное качество за счет большого размера пикселей.

Технология Super Pixel (Quad Pixel, Quad Bayer, TetraCell)

Достигнув огромного разрешения (48 мегапикселей, 64 мегапикселя и более), компании начали искать другие способы дальнейшего улучшения камеры.В результате была разработана технология Super Pixel с использованием Pixel Binning. Фактически, этот алгоритм объединяет четыре маленьких пикселя в один большой пиксель с помощью фильтров.

Практически все лидеры используют эту технологию. Sony называет это Quad Bayer, Samsung использует термин TetraCell.

Смешивание пикселей устраняет проблему недостаточного освещения. Алгоритм объединяет данные RAW из четырех пикселей в один эффективный суперпиксель, обеспечивая максимальное количество захваченного света при одновременном снижении шума изображения.

Конечно, это снижает реальное разрешение изображения. Например, 24-мегапиксельная камера с технологией Super Pixel может обеспечить реальное разрешение всего 6 мегапикселей. Поэтому камеры с низким разрешением редко используют эту опцию. Его эффективность проявляется в 40-мегапиксельных матрицах и выше. В этом случае алгоритм улучшает качество в условиях низкой освещенности за счет уменьшения чрезмерного разрешения.

Помимо уменьшения разрешения, эта технология также исключает вывод в формате RAW (DNG) из-за потери данных во время объединения пикселей.

OIS и автофокус

Многие современные камеры используют OIS (оптическую стабилизацию изображения) для повышения четкости и улучшения фокусировки при съемке в движении или при слабом освещении.

Фактически, OIS обеспечивает амортизацию для компенсации перемещений камеры во время движения. Механизм оптической стабилизации сглаживает дрожание рук или движение при ходьбе. Функционально OIS заменяет традиционный штатив.

В бюджетных моделях часто используется цифровая стабилизация вместо более эффективной и дорогой оптической стабилизации.В этом случае алгоритм сглаживает градации размытых кадров.

Кроме того, почти все современные фотоаппараты имеют автофокусировку на одном или нескольких объектах. Сегодня компании используют контрастный, фазовый и лазерный автофокус. Но лазерный автофокус обеспечивает максимальную эффективность.

Вывод

1. Разрешение датчиков изображения в камерах смартфонов практически достигло максимума. Его дальнейшее увеличение уже ограничено уменьшением захваченного света из-за уменьшения размера пикселя.Судя по всему, дальнейшее совершенствование камер будет основано на увеличении размера матрицы и улучшении алгоритмов обработки сигналов.

2. С другой стороны, даже среднебюджетные модели обеспечивают достаточно высокое качество для любительской фотографии. Многие дорогие смартфоны уже успешно конкурируют с традиционными камерами за качество изображения.

В этом видео демонстрируется новейший инновационный датчик изображения Sony IMX686 для смартфонов.

Понимание матрицы камеры — OpenCV Q&A Forum

Привет всем,

Я использовал процедуру калибровки шахматной доски для получения матрицы камеры с использованием OpenCV и python на основе этого руководства: http: // opencv-python -Tutroals. readthe …

Я просмотрел пример кода на этой странице и смог воспроизвести их результаты с изображениями шахматной доски в папке OpenCV, чтобы получить матрицу камеры.

Затем я попробовал ту же процедуру с моей собственной шахматной сеткой и камерой, и я получил следующую матрицу:

mtx = [1535 0 638 0 1536 204 0 0 1]

Я пытаюсь лучше понять эти результаты, основываясь на датчике камеры и объективе, которые я использую.

По материалам: http: // ksimek.github.io/2013/08/13/in …

Fx = fx * W / w

Fx = фокусное расстояние в мм W = ширина сенсора в мм w = ширина изображения в пикселях fx = фокусное расстояние в пикселях

Размер моих изображений: 1264 x 512 (ширина x высота) Я использую следующий объектив: http: //www.edmundoptics.com/imaging/i …

У него фокусное расстояние 8 мм.

Я использую камеру FL3-U3-13Y3 от PtGrey (https: //www.ptgrey.com/flea3-13-mp-mo …), у которой ширина изображения 12 мм, согласно этому изображению. :

В матрице камеры fx — это элемент в первой строке, первом столбце.Итак, выше, fx = 1535. Короче:

fx = 1535 пикселей (из матрицы камеры я получил) w = 1264 пикселя (размер изображения я установил) W = 12 мм (из таблицы) Fx = 8 мм (из таблицы)

Используя: Fx = fx * W / w, можно было бы ожидать Fx = 1535 * 12/1264 = 14,57 мм

Но реальный объектив 8 мм. Почему несоответствие?

Я бы подумал, что необходимо знать фактический размер шахматной сетки, но я не видел упоминания о манипуляциях с ней в предоставленной мной ссылке на руководство.Мне в основном пришлось уменьшить сетку шахматной доски, чтобы она работала с моей камерой.

Я был бы признателен за любую помощь или понимание по этому поводу.

Заранее спасибо

РЕДАКТИРОВАТЬ: На самом деле, если быть более конкретным, объектив имеет максимальный формат сенсора камеры 1/3 дюйма, а формат сенсора камеры — 1/2 дюйма. Я нашел статью об этом: http: //www.cambridgeincolour. com/tuto …

Множитель фокусного расстояния = (1/2) / (1/3) = 1,5 Фокусное расстояние объектива, указанное в таблице данных = 8 мм. Эквивалентное фокусное расстояние объектива = 1.5 * 8 мм = 12 мм

Тем не менее, 12 мм отличается от 14,57 мм. Не учитываю ли я что-то еще в своих расчетах? Может ли это происходить из-за плохих изображений, которые все еще попадают в углы шахматной доски?

Ниже приведен пример изображения:

Внутренняя калибровка

Внутренняя калибровка
следующий: Движение камеры Up: Модель камеры Предыдущий: Простая модель & nbsp Содержание

На реальной камере фокусное расстояние (т.е.е. расстояние между центром проекции и плоскостью сетчатки) будет отличаться от 1, поэтому координаты уравнения (3.2) должны быть масштабированы, чтобы принять это во внимание.

Кроме того, координаты на изображении не соответствуют физическим координатам в плоскости сетчатки. В случае камеры CCD соотношение между ними зависит от размера и формы пикселей, а также от положения кристалла CCD в камере. Для стандартной фотокамеры это зависит от процесса сканирования, посредством которого изображения оцифровываются.

Преобразование показано на рисунке 3.3. Координаты изображения получаются с помощью следующих уравнений:

где и — ширина и высота пикселей, — главная точка и угол перекоса, как показано на рисунке 3.3. Поскольку важны только отношения и, в оставшейся части текста будут использоваться упрощенные обозначения следующего уравнения:

(C3)

где и является фокусным расстоянием, измеряемым по ширине и высоте пикселей, и фактором, учитывающим перекос из-за непрямоугольных пикселей.Вышеупомянутая верхняя треугольная матрица называется калибровочной матрицей камеры; и для этого будут использоваться обозначения. Итак, следующее уравнение описывает преобразование координат сетчатки в координаты изображения.

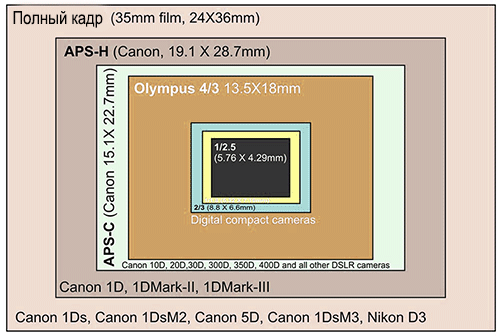
(C4)

Для большинства камер пиксели почти идеально прямоугольные и поэтому очень близки к нулю. Кроме того, главная точка часто находится близко к центру изображения. Эти предположения можно часто использовать, конечно, для получения подходящей инициализации для более сложных итеративных процедур оценки.

Рисунок 3.3: От координат сетчатки к координатам изображения

Для камеры с фиксированной оптикой эти параметры идентичны для всех изображений, сделанных камерой. Для камер с возможностью масштабирования и фокусировки фокусное расстояние, очевидно, может меняться, но также может меняться главный момент. Обширное обсуждение этого вопроса можно найти, например, в работе Уилсона [173, 171, 172, 174].

---

следующий: Движение камеры Up: Модель камеры Предыдущий: Простая модель & nbsp Содержание

Марк Поллефейс 2002-11-22

Внутренние параметры камеры для набора изображений с измененным размером шахматной доски

Я понял, что удобнее изменять размер (уменьшать) изображение входной камеры до небольшого стандартного размера (в моем случае 320 x 240) вместо того, чтобы каждый раз изменять параметры в соответствии с размером изображения каждой камеры. То есть исходное большое изображение и его внутренние параметры просто используются для отображения визуализированной сцены дополненной реальности, а вся последующая обработка выполняется с измененным размером изображения и соответствующими внутренними параметрами.

В основном внутренние параметры камеры необходимы для расчета проекции трехмерной точки на плоскость изображения. Такая проекция, по-видимому, является важной частью визуального SLAM, как прогнозирование наблюдения за трехмерными ориентирами для текущего кадра на основе положения камеры и оценки трехмерной карты предыдущего кадра.

Итак, чтобы получить изображение с измененным размером, все, что мне нужно сделать, это использовать функцию cv :: resize () OpenCV. Для соответствующих внутренних параметров мне нужно что-то сделать. Мне нужно создать внутренние параметры виртуальной камеры из физически существующей и откалиброванной камеры.

Интуитивно понятно, что среди внутренних параметров фокусное расстояние и главная точка изображения с измененным размером могут быть вычислены путем простого масштабирования как коэффициента изменения размера. Например, если исходное изображение камеры — 1280 x 960, а изображение с измененным размером — 320 x 240, соотношение равно 1/4, а фокусное расстояние и главная точка масштабируются таким образом.

А как насчет коэффициентов искажения? Должен ли я масштабировать их как фокусное расстояние и главную точку? Я разместил следующий вопрос на доске сообщества visual slam в Google plus, и Хосе Херонимо Морейра Родригес дал мне ответ, в котором говорится, что «факторы искажения остаются прежними из-за их определений». Спасибо, Родригес.

Мой вопрос:

Допустим, у меня есть изображения шахматной доски размером w (ширина) и h (высота). (Обратите внимание, что w и h — это не фактический размер шахматной доски, а размер изображения шахматной доски.)
После калибровки камеры (Чжан) результирующие внутренние параметры камеры: fx (фокусное расстояние x), fy (фокусное расстояние y), cx (главная точка x), cy (главная точка y), k1 (1-й коэффициент искажения), k2 (2-й коэффициент искажения), k3 (3-й коэффициент искажения), k4 (4-й коэффициент искажения), k5 (5-й коэффициент искажения).
Если я изменю размер изображений шахматной доски вдвое, так что ширина и высота изображений с измененным размером будут w / 2 и h / 2 соответственно, и снова проведу калибровку камеры, я теоретически ожидаю получить fx / 2, fy / 2, cx / 2 и cy / 2 как фокусное расстояние x, фокусное расстояние y, главная точка x и главная точка y соответственно.
А как насчет коэффициентов искажения? Что я ожидал теоретически получить 1-й, 2-й, 3-й, 4-й и 5-й коэффициенты искажения измененных изображений шахматной доски с точки зрения k1, k2, k3, k4 и k5?

Родригес:

Они не меняются. Они являются функцией X / Z и Y / Z. Проверьте http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/parameters.html. Меняется только собственная матрица, но не коэффициенты искажения.

Эксперимент с использованием набора инструментов калибровки камеры для Matlab с изображениями шахматной доски в папке примеров OpenCV также показывает, что коэффициенты искажения НЕ меняются.
Я провел эксперимент, создав два набора изображений (1280 x 960 и 320 x 240) из исходных изображений шахматной доски (640 × 480) в папке примеров OpenCV. Результат

1280 x 960 (двойной)
Фокусное расстояние: fc = [1074.34831 1073.83567]
Основная точка: cc = [653.70628 499.16838]
Искажение: kc = [-0,28805 0,10555 -0,00083 0,00033 0,00000] 640 x 480 (исходное)
Фокусное Длина: fc = [536.93593 536.52653]
Основная точка: cc = [326.87081 249,24606]
Искажение: kc = [-0,28990 0,10780 -0,00079 0,00017 0,00000]
320 x 240 (половина)
Фокусное расстояние: fc = [268,65196 268,42076]
Основная точка: cc = [162,95051 124,58663] kc =
[Искажение] -0,29024 0,10502 -0,00072 -0,00004 0,00000]

…

Нравится:

Нравится Загрузка …

Связанные

Что такое калибровка камеры? — MATLAB и Simulink

Что такое калибровка камеры?

Геометрическая калибровка камеры , также называемая камерой резекционирование , оценивает параметры линзы и датчика изображения изображение или видеокамера. Вы можете использовать эти параметры для коррекции искажения объектива, измерения размер объекта в мировых единицах или определение положения камеры в сцене. Эти задачи используются в таких приложениях, как машинное зрение, для обнаружения и измерения объектов. Они также используются в робототехнике, для навигационных систем и реконструкции трехмерных сцен.

Примеры того, что вы можете сделать после калибровки камеры:

Параметры камеры включают внутренние, внешние и коэффициенты искажения.Чтобы оценить параметры камеры, вам необходимо иметь трехмерные мировые точки и соответствующие им двумерные изображения точки. Вы можете получить эти соответствия, используя несколько изображений калибровочного шаблона, например, шахматная доска. Используя соответствия, вы можете найти параметры камеры. После калибровки камеры для оценки точности предполагаемых параметров вы можете:

• Постройте относительное расположение камеры и калибровочного шаблона.

• Рассчитайте ошибки перепроецирования.

• Рассчитайте ошибки оценки параметров.

Используйте калибратор камеры для калибровки камеры и оценить точность предполагаемых параметров.

Модели камер

Computer Vision Toolbox ™ содержит алгоритмы калибровки для модели камеры-обскуры и Рыбий глаз модель камеры.

Алгоритм калибровки крошечного отверстия основан на модели, предложенной Жаном-Ивом Буге. [3].Модель включает в себя модель камеры-обскуры [1] и искажение объектива [2]. Модель камеры-обскуры не учитывает искажение объектива, потому что идеальная Камера-обскура не имеет объектива. Чтобы точно представить реальную камеру, полный модель камеры, используемая алгоритмом, включает радиальную и тангенциальную линзы искажение.

Из-за сильного искажения, производимого линзами рыбий глаз, модель с отверстиями не может смоделировать камеру рыбий гл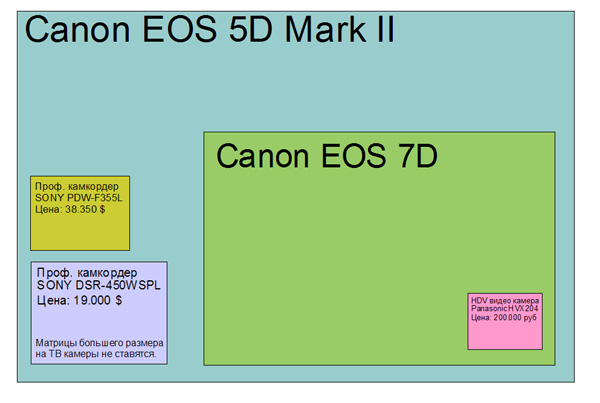аз. Подробнее о калибровке камеры с использованием модели «рыбий глаз» см. Основы калибровки «рыбий глаз».

Камера-обскура Модель

Камера-обскура — это простая камера без объектива и с одной маленькой апертурой. Лучи света проходят через апертуру и проецируют перевернутое изображение на противоположной стороне. камеры. Думайте о плоскости виртуального изображения как о находящейся перед камерой и содержащее вертикальное изображение сцены.

Параметры камеры-обскуры представлены в матрице 4 на 3, называемой матрица камеры .Эта матрица отображает трехмерную мировую сцену в плоскость изображения. Алгоритм калибровки рассчитывает матрицу камеры с использованием внешнего и внутренние параметры. Внешние параметры представляют местоположение камеры. в 3-D сцене. Внутренние параметры представляют собой оптический центр и фокусное расстояние. камеры.

Мировые точки преобразуются в координаты камеры с помощью внешние параметры.Координаты камеры отображаются в плоскости изображения с помощью внутренние параметры.

Параметры калибровки камеры

Алгоритм калибровки рассчитывает матрицу камеры с использованием внешних и внутренние параметры. Внешние параметры представляют собой жесткую трансформацию из 3-D мировую систему координат в систему координат трехмерной камеры. Внутренние параметры представляют собой проективное преобразование трехмерных координат камеры в двухмерные координаты изображения.

Внешние параметры

Внешние параметры состоят из вращения, R, и перевод, т . Начало системы координат камеры в его оптическом центре и оси x- и y- определить плоскость изображения.

Внутренние параметры

Внутренние параметры включают фокусное расстояние, оптический центр, также известный как основная точка и коэффициент перекоса. Камера собственная матрица, K , определяется как:

Перекос пикселей определяется как:

[cxcy] — Оптический центр (основная точка), дюйм пикселей.

(fx, fy) — Фокусное расстояние в пикселях. fx = F / px fy = F / py F — Фокусное расстояние в мировых единицах, обычно выражается в миллиметрах. (px, py) — Размер пикселя в мировых единицах.

s — Коэффициент перекоса, который не равен нулю, если изображение оси не перпендикулярны. s = fxtanα

Искажение при калибровке камеры

Матрица камеры не учитывает искажение объектива, поскольку идеальная камера-обскура нет линзы. Чтобы точно представить реальную камеру, модель камеры включает радиальная и тангенциальная линзовые искажения.

Радиальное искажение

Радиальное искажение возникает, когда световые лучи изгибаются ближе к краям линзы, чем они делают в его оптическом центре. Чем меньше объектив, тем больше искажение.

Радиальная деформация коэффициенты моделируют этот тип искажения. Искаженные точки обозначается как ( x _{искажено} , y _{искажено} ):

x _{искажено} = x (1 + k ₁ * r ² + k ₂ * r ⁴ + k ₃ * r ⁶

017

9000 = y (1 + k ₁ * r ² + k ₂ * r ⁴ + k ₃ * r ⁶ )

• x , y — Неискаженное расположение пикселей. x и y являются в нормализованных координатах изображения. Нормализованные координаты изображения вычисляется из координат пикселей путем перевода в оптический центр и деление на фокусное расстояние в пикселях. Таким образом, x и y являются безразмерный.

• к ₁ , к ₂ , и k ₃ — Радиальное искажение коэффициенты линзы.

• r ² : x ² + y ²

Обычно для калибровки достаточно двух коэффициентов.Для сильного искажения, например, в широкоугольных объективах, вы можете выбрать 3 коэффициента, включающих k ₃ .

Тангенциальное искажение

Тангенциальное искажение возникает, когда линза и плоскость изображения не параллельны. Коэффициенты тангенциального искажения моделируют это тип искажения.

Искаженное точки обозначаются как ( x _{искажено} , y _{искажено} ):

x _{искажено} = x + [2 * p ₁ * x * y + p ₂ * ( r ² + 2 * x ² )]

y _{искажено} = y + [ p ₁ * ( r ² + 2 * y ² ) + 2 * p ₂ * x * y ]

• x , y — Неискаженное расположение пикселей. x и y являются в нормализованных координатах изображения. Нормализованные координаты изображения вычисляется из координат пикселей путем перевода в оптический центр и деление на фокусное расстояние в пикселях. Таким образом, x и y являются безразмерный.

• п. ₁ и п. ₂ — Коэффициенты тангенциального искажения объектива.

• r ² : х ² + y ²

Ссылки

[1] Zhang, Z.«Новая гибкая техника для камеры Калибровка ». IEEE Transactions on Pattern Analysis and Machine Разведка 902 18. Vol. 22, № 11, 2000, с. 1330–1334.

[2] Хейккила Дж. И О. Силвен. «Четырехступенчатая камера Процедура калибровки с неявной коррекцией изображения ». IEEE Международная конференция по компьютерному зрению и паттернам Признание . 1997.

[4] Брадски Г. и А. Келер. Изучение OpenCV: Компьютерное зрение с библиотекой OpenCV .Севастополь, Калифорния: О’Рейли, 2008.

См. Также

Приложения

Связанные темы

Модуль: tfg.rendering.camera.perspective | Графика TensorFlow

Посмотреть исходный код на GitHub

Этот модуль реализует функции перспективной камеры.

Модель перспективной камеры, также называемая моделью камеры-обскуры, определяется с использованием фокусного расстояния \ ((f_x, f_y) \) и главной точки \ ((c_x, c_y) \).Модель перспективной камеры можно записать как калибровочную. матрица

$$ \ mathbf {C} = \ begin {bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \ end {bmatrix},

$

также называется матрицей внутренних параметров. Фокусное расстояние камеры \ ((f_x, f_y) \), определяемое в пикселях, — это физическое фокусное расстояние, деленное на физический размер пикселя камеры. Физическое фокусное расстояние — это расстояние между центром камеры и плоскостью изображения.Главное — это пересечение оси камеры с плоскостью изображения. Ось камеры — это линия, перпендикулярная плоскости изображения, начиная с оптического центра.

Более подробную информацию о перспективных камерах можно найти на этой странице.

Примечание: Текущая реализация не учитывает искажения или параметры перекоса.

Функции

intrinsics_from_matrix (...) : извлекает внутренние параметры из калибровочной матрицы.

matrix_from_intrinsics (...) : Строит калибровочную матрицу из внутренних параметров.

parameters_from_right_handed (...) : восстанавливает параметры, используемые для построения матрицы правой проекции.

проект (...) : проецирует трехмерную точку на двумерную плоскость камеры.

луч (...) : вычисляет трехмерный луч для двухмерной точки (z-компонент луча равен 1).

right_handed (...) : Создает матрицу для правой перспективной проекции.

unproject (...) : спроецировать 2-ю точку в 3-м.

Модель проекционной камеры

| imatest

Не рекомендуется в текущей версии

---

Модель проекционной камеры описывает математику преобразования мировой точки в точку изображения. Это делается с помощью модели камеры с отверстиями. Вместе с моделью искажения, которая характеризует отклонение от модели точечного отверстия, этим методом можно моделировать большинство камер *.j \ left (\ mathbf {X} _ {i} \ right) \)

Есть три компонента для применения модели проективного преобразования: внешние элементы, модель камеры-точечного отверстия и искажение точек для учета разницы между встроенной камерой и моделью-крошечным отверстием.

Проекция трехмерных точек в модели камеры-обскуры.

Изображение проецируемых точек.

Внутренние функции камеры описывают свойства модели камеры-обскуры, которые связывают относительные мировые координаты камеры относительно камеры с координатами изображения.В модели крошечного отверстия лучи проходят по прямой линии от объекта в сцене через крошечное отверстие к фокальной плоскости. Геометрия этого подобна треугольникам, связывающим мировые координаты с координатами изображения. Математическая модель для этого использует 5 параметров: фокусное расстояние в направлениях x и y, основная точка в направлениях x и y и перекос между направлениями x и y.

Параметры

Фокусное расстояние

В модели точечного отверстия фокусное расстояние \ (f \) — это расстояние от отверстия до фокальной плоскости вдоль оптической оси.Системы с большим фокусным расстоянием будут иметь большее увеличение в более узком поле зрения (FOV), тогда как меньшие фокусные расстояния будут иметь больший охват.

Возможно иметь разное фокусное расстояние вдоль каждого направления фокальной плоскости. В этом случае фокусное расстояние оси \ (y \) изменяется на \ (\ alpha \).

\ (f_y = \ alpha \ cdot f \)

Для настоящей камеры-обскуры \ (f_x = f_y \) (\ (\ alpha = 1 \)), однако на практике это может быть связано с факторами, включая производственные дефекты, искажение объектива и изображения, полученные с помощью системы сканирования.Интерпретация неравных фокусных расстояний заключается в том, что эффективная форма пикселя не является квадратной.

Принцип действия

Точка \ ((pp_x, pp_y) \) является основной точкой, которая представляет собой пиксельную координату пересечения оптической оси с фокальной плоскостью. Функция сдвига наклона-сдвига перемещает фокальную плоскость (и главную точку) вокруг оптической оси.

Косой

Фактор перекоса \ (s \) вводит трансформацию сдвига изображения.Для многих камер это 0. Случаи, когда оно не равно нулю, включают в себя фотографирование изображения (введение гомографии) и несинхронизацию процесса выборки пикселей из фреймграббера. Ненулевой перекос означает, что оси x и y камеры не перпендикулярны друг другу.

Внутренняя матрица

Внутренняя матрица, \ (\ mathbf {K} \) — это верхнетреугольная матрица, которая преобразует мировую координату относительно камеры в координату однородного изображения. Существует две общие и эквивалентные формы внутренней матрицы:

\ (\ mathbf {K} = \ begin {bmatrix} f & s & pp_x \\ 0 & f \ cdot \ alpha & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)

\ (\ mathbf {K} = \ begin {bmatrix} f_x & s & pp_x \\ 0 & f_y & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)

Многие камеры могут быть представлены с более простой внутренней матрицей.Если перекос равен 0:

\ (\ mathbf {K} = \ begin {bmatrix} f_x & 0 & pp_x \\ 0 & f_y & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)

Если перекос равен 0 и \ (\ alpha = 1 \):

\ (\ mathbf {K} = \ begin {bmatrix} f & 0 & pp_x \\ 0 & f & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)

Внутренняя матрица камеры \ (j \) ^th применяется к точке 3D \ (i \) ^th относительно камеры, чтобы создать точку однородного изображения.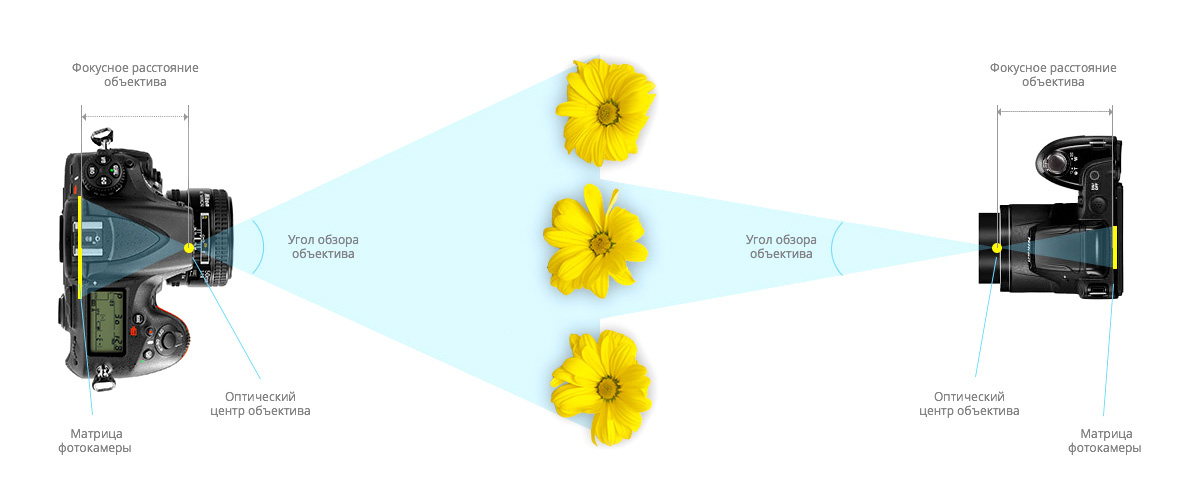 \ top \) будет точкой относительно камеры.Предположим, что

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ begin {bmatrix} f & 0 & pp_x \\ 0 & f & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \ begin {bmatrix} X \\ Y \\ Z \ end {bmatrix} \)

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ begin {bmatrix} f \ cdot X + pp_x \ cdot Z \\ f \ cdot Y + pp_y \ cdot Z \\ Z \ конец {bmatrix} \)

После преобразования в неоднородные координаты

\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ displaystyle \ frac {f \ cdot X + pp_x \ cdot Z} {Z} \\ \ displaystyle \ frac { е \ cdot Y + pp_y \ cdot Z} {Z} \ end {bmatrix} = \ begin {bmatrix} f \ cdot \ displaystyle \ frac {X} {Z} + pp_x \\ f \ cdot \ displaystyle \ frac {Y } {Z} + pp_y \ end {bmatrix} \)

Проверка этого результата показывает, что расстояние от оптической оси (основной точки) пропорционально отношению расстояния мировых точек от оптической оси к расстоянию до камеры.Это означает, что точка, которая вдвое дальше от оптической оси и вдвое дальше от камеры, будет соответствовать той же точке изображения. Лучшая реконструкция точки с помощью одной камеры — это то, что точка находится где-то на линии.

Квартир

Все эти значения рассчитываются в единицах количества пикселей. Шаг пикселя \ (p \) используется для преобразования количества пикселей в физические единицы. Например:

\ (f [\ mathrm {mm}] = f [\ mathrm {пикселей}] \ cdot p \ left [\ frac {\ mu \ mathrm {m}} {\ mathrm {pixel}} \ right] \ cdot \ гидроразрыв {1 [\ mathrm {mm}]} {1000 [\ mu \ mathrm {m}]} \)

Обратный

Инверсия внутренней матрицы камеры используется для преобразования неискаженных точек изображения в линии от центра камеры.{-1} = \ displaystyle \ frac {1} {f} \ begin {bmatrix} 1 & 0 & -pp_x \\ 0 & 1 & -pp_y \\ 0 & 0 & f \ end {bmatrix} \)

Модель искажения камеры описывает отклонение физической камеры от модели проекционной камеры. Он преобразует неискаженные точки 2D-изображения в точки искаженного 2D-изображения (те, что находятся за пределами камеры). Модель обратной дисторсии преобразует точки искаженного изображения в неискаженные.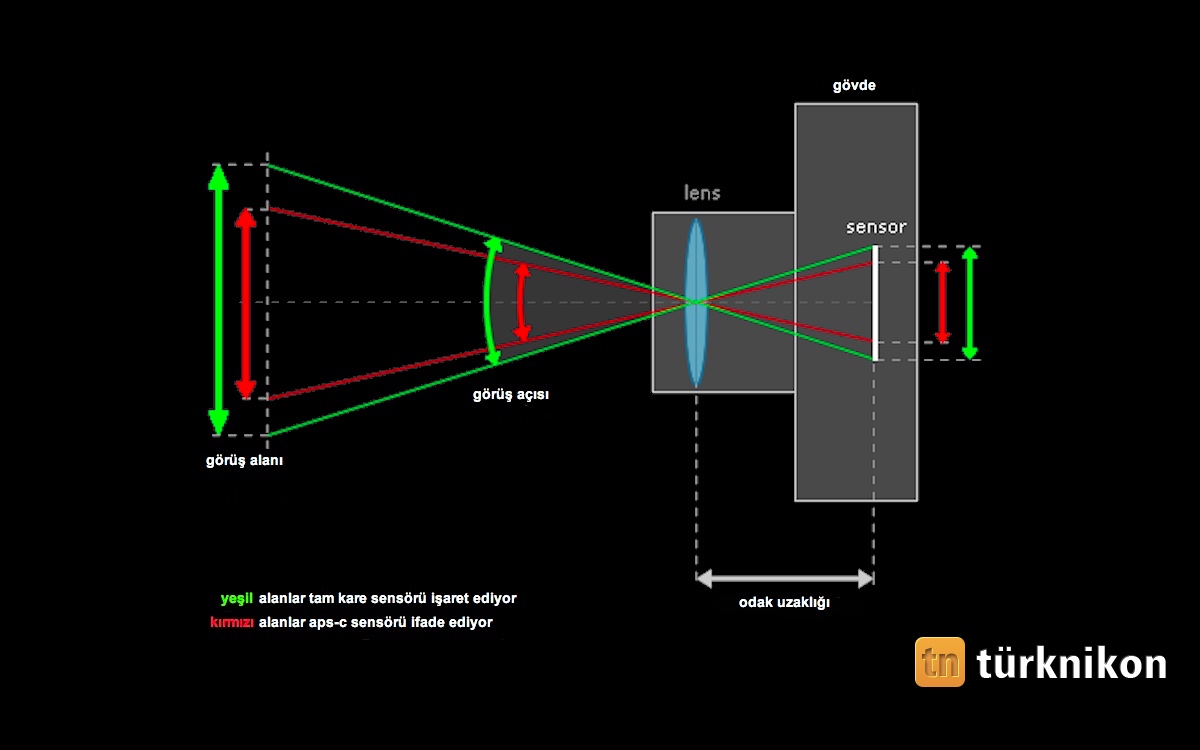

Внешний вид камеры описывает положение и ориентацию камеры в мире.Существует два способа описания преобразования координат между мировыми координатами и координатами относительно камеры: преобразование точки и преобразование осей (поза). Они оба имеют одну и ту же форму матрицы вращения / переноса и являются противоположными друг другу.

Центр камеры соответствует расположению входного зрачка камеры. В панорамной фотографии это часто называют точкой отсутствия параллакса. Камеры с большим полем зрения (например, камеры «рыбий глаз») будут иметь разные положения входного зрачка при разных углах поля зрения.Для этих камер используется осевое расположение входного зрачка.

Точечное преобразование

Описание преобразования точки преобразует мировую точку в точку относительно камеры. Его матрица вращения / переноса прямо умножается вправо на внутреннюю матрицу для формирования матрицы камеры.

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right] \ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ end {array} \ right] \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)

В обозначении точечного преобразования камера расположена в \ (- \ mathbf {R} ^ \ top \ mathbf {t} \). {\ top} \ mathbf {t} \\ &&& \ end {array} \ right] \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)

В обозначении позы камеры центр камеры расположен в \ (\ mathbf {t} \).

Матрица камеры \ (\ mathbf {P} \) представляет собой комбинацию внутренней матрицы камеры и точечного преобразования.

\ (\ mathbf {P} = \ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right] \ left [\ begin {array} { ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ end {array} \ right] \)

Матрица камеры преобразует точки мира в координаты однородного изображения.

Мировые точки к точкам изображения

1. Преобразование мировой координаты в координату относительно камеры путем умножения на мировую точку в преобразование точки изображения.Это преобразование является обратным позы.
2. Примените внутреннюю матрицу камеры к относительной координате камеры, чтобы получить однородную координату изображения.
3. Преобразует координату однородного изображения в неоднородную координату.
4. Примените модель искажения, чтобы определить положение изображения мировой точки на фокальной плоскости.

Обозначение преобразования точек

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ underbrace {\ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right]} _ {\ mathrm {intrinics}} \ underbrace {\ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ конец {массив} \ right]} _ {\ mathrm {инверсия \ позы}} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)

\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ mathrm {distort} _ {x} \! \! \ Left (\ displaystyle \ frac {x} {w } \ right) \\\ mathrm {искажать} _ {y} \! \! \ left (\ displaystyle \ frac {y} {w} \ right) \ end {bmatrix} \)

Обозначение преобразования осей

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ underbrace {\ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right]} _ {\ mathrm {intrinics}} \ underbrace {\ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} ^ {\ top} && — \ mathbf { R} ^ {\ top} \ mathbf {t} \\ &&& \ end {array} \ right]} _ {\ mathrm {inverse \ pose}} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ конец {bmatrix} \)

\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ mathrm {distort} _ {x} \! \! \ Left (\ displaystyle \ frac {x} {w } \ right) \\\ mathrm {искажать} _ {y} \! \! \ left (\ displaystyle \ frac {y} {w} \ right) \ end {bmatrix} \)

Изображение указывает на линии

1. Примените модель обратной дисторсии, чтобы неискажать точки изображения.

   No related posts.